Professor Kučera has resolved a long-standing open problem of linear systems theory – decoupling by static state feedback. The earliest known investigation of system decoupling dates back to 1934, a state space formulation of the problem appeared in 1964, and a solution for square and invertible systems followed in 1967. The general case of right invertible systems, however, has withstood all past efforts to obtain a solution.
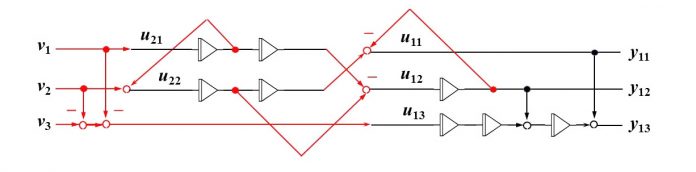
Decoupling is a problem of compensating a given system in such a way that each system output can be independently controlled by a corresponding system input. Such a structure is desirable in a number of applications, since considerable conceptual simplicity can be accrued for subsequent system design. Decoupling can always be achieved using dynamic compensation, which increases the order of the system. The static state feedback, however, does not increase the order and therefore may involve only the internal dynamics.
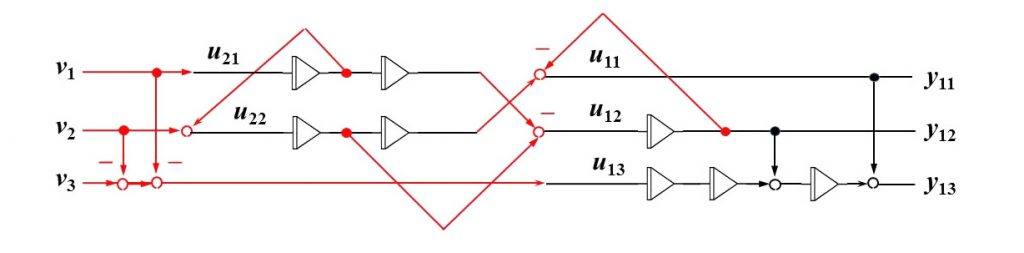
A solution of this very complex problem is presented for the very first time. The formulation avoids restrictive hypotheses concerning system and decoupling feedback. The existence of a solution is shown to depend on the existence of three lists of nonnegative integers conditioned by and only by system invariants with respect to the permissible transformations. The solvability conditions are necessary and sufficient. The necessity proof is based on existence results whereas the sufficiency proof is based on constructive arguments and provides an algorithm to determine a decoupling feedback.
The result will appear as Paper in the December 2017 issue of the prestigious journal IEEE Transactions on Automatic Control.