Na mezinárodním šampionátu CADE ATP System Competition (CASC) opět zazářil automatický dokazovač Vampire. Nová, vylepšená verze, Vampire 4.9, dosáhla vynikajících výsledků a zvítězila v šesti ze sedmi vypsaných kategorií. Na vývoji Vampire a jeho nové verze se významně podílel Martin Suda, vedoucí týmu automatického uvažování na CIIRC, který do Vampire 4.9 mimo jiné implementoval nové strategie.
O šampionátu v automatickém uvažování
CADE ATP System Competition, organizovaný Dr. Geoffem Sutcliffem z Univerzity v Miami, je součástí mezinárodní konference automatického uvažování IJCAR. Letos jubilejní, 30. ročník soutěže se konal v termínu 1. – 6. července 2024 ve francouzském městě Nancy. Šampionát představuje soutěž, kde naprogramované systémy s prvky umělé inteligence řeší komplexní matematické problémy formulované ve strojově srozumitelném jazyce matematické logiky. Cílem je vyřešit co nejvíce problémů v časovém limitu tří nebo pěti minut.
V letošním ročníku soutěže se Vampire zúčastnil všech sedmi kategorií. Verze Vampire 4.9 uspěla ve všech kategoriích kromě kategorie Typed First-order Non-theorems, kde ji překonal dokazovač iProver 3.9, ale pouze v počtu formálně uznaných řešení. Proto je výsledek považován za velký úspěch a tým Martina Sudy doufá, že v příštím roce zvítězí již ve všech kategoriích.
RNDr. Martin Suda, PhD., který navrhl nové strategie pro verzi Vampire 4.9, považuje tento výsledek za velmi dobrý a těší se na další výzvy. „Automatické hledání silných a vzájemně se doplňujících dokazovacích strategií je velmi zajímavá algoritmická úloha, k jejíž řešení jsme letos též přispěli novým článkem, publikovaným právě na IJCARu,“ říká. „Zabývali jsme tím, jak zařídit, aby nové strategie, které typicky objevujeme jako ‚specialisty‘ pro nějaký konkrétní problém, zároveň generalizovaly a s velkou šancí řešily problémy nové, při tréninku neznámé.“
Tento rok byly soutěžní kategorie následující:
- High-order Theorems
- Typed First-order Theorems
- Typed First-order Non-theorems
- First-order Theorems
- Unit Equality CNF
- Sledge Hammer Theorems
- I Challenge yoU
Jednou z novinek letošního ročníku byla kategorie I Challenge U, do které týmy zasílaly 10 náročných problémů, které měly za cíl otestovat schopnosti ostatních dokazovacích systémů. Vampire 4.9 v této kategorii exceloval, když vyřešil 59 problémů z 80, což ho vyneslo na první místo.
Vampire 4.8, předchozí verze systému, dosáhl v minulém roce soutěže skvělých výsledků v kategoriích jako First-order Non-theorems a Higher-order Theorems. Letošní verze, Vampire 4.9, přinesla zlepšení i díky novým strategiím vyvinutým právě Martinem Sudou z našeho institutu. Na vývoji se také významně podílel Ahmed Bhayat z Univerzity v Manchesteru, který je hlavní autor podpory pro logiku vyššího řádu (higher-order logic).
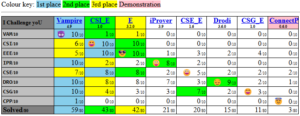
V tabulce níže, která zobrazuje podrobné výsledky letošní soutěže, je též možné nalézt porovnání s vítězi divizí z minulého roku (viz systémy označené růžovou barvou). Zlepšení nového Vampire 4.9 je znatelné. Například v kategorii High-order Theorems zvládl oproti minulému roku vyřešit o 16 problémů více, což Martin Suda považuje za úspěch. Vampire 4.9 letos v této kategorii vyřešil 463 problémů z 500 zadaných. Dokazovač Zipperposition, který se umístil jako druhý, vyřešil pouze 433 problémů z 500.

V letošním roce došlo v divizi First-order Theorems k obrovskému zlepšení oproti loňskému vítězi Vampire 4.8, konkrétně o více než 100 problémů. Podle Martina Sudy je to z velké části zásluha včasného zaslání dokazovače před soutěží pro tak zvanou problem ranking fázi: „Soutěž má pravidlo, podle kterého mohou být vybrány pouze problémy, které mají šanci být alespoň nějakým systémem vyřešeny. Problem ranking je proces, při kterém organizátor takovou množinu problému určí (a nakonec z nich nějaký počet vybere pro soutěž.) Tím, že jsme letos Vampire přihlásili včas, do osudí se dostalo mnoho problémů, které umí vyřešit, díky našim novým strategiím, jenom Vampire.“
Výkon v divizi Unit Equality CNF se také velmi zlepšil. Dokonce natolik, že Vampire 4.9 poprvé v soutěži zvítězil. To bylo umožněno přidáním řady optimalizací jako například vylepšení indexovacích technik, líného vyhodnocování některých operací a běhové specializace operace porovnávání logických termů. Velkou zásluhu na tomto výsledku má Martinův kolega Márton Hajdu z TU Wien.

Budoucnost a výzvy týmu Vampire
Martin Suda a jeho tým plánují pokračovat ve vývoji a vylepšování dokazovače Vampire, aby v příštím roce zvítězil ve všech kategoriích. Motivace a nadšení týmu jsou klíčové pro další pokroky v oblasti automatického dokazování, které může přinést revoluční aplikace v různých vědeckých a technických oborech.
Automatické dokazování není jen soutěž algoritmů, ale má široké aplikace v praxi. Dokazovače jako Vampire mohou usnadnit práci matematikům, programátorům a designérům systémů. Obzvláště důležité jsou v oblastech, kde je klíčová spolehlivost, například v medicíně nebo dopravě, kde na správném fungování systémů závisí lidské životy.
Držíme palce Martinu Sudovi a jeho týmu v jejich úsilí a těšíme se na další skvělé výsledky v budoucnu.



